Units and measurements are the backbone of physics. They allow scientists to quantify and understand the physical world. In this article, we will explore the basics of units and measurements in physics, including physical quantities, fundamental physical quantities, the International System of Units (SI units), derived physical quantities and units, physical quantities without units, and multiples and submultiples of units.
Physical quantities and units:
A physical quantity is a quantity that can be measured and expressed as a numerical value. Examples of physical quantities include length, mass, time, temperature, and electric charge. Units are the standardized measurements used to express these physical quantities. Units enable scientists to make precise and accurate measurements and communicate them to others in a way that is universally understood.
Fundamental physical quantities:
Fundamental physical quantities are the most basic physical quantities that cannot be expressed in terms of other physical quantities. There are seven fundamental physical quantities in the SI system: length, mass, time, electric current, temperature, amount of substance, and luminous intensity. These quantities are used to define all other physical quantities.
International System of Units (SI units):
The SI system is the most widely used system of units in science. It is based on seven fundamental physical quantities and uses a combination of base units and supplementary units to express all other physical quantities.
Base units:
Base units are the fundamental units used to express the seven fundamental physical quantities. The base units in the SI system include the meter (m) for length, the kilogram (kg) for mass, the second (s) for time, the ampere (A) for electric current, the kelvin (K) for temperature, the mole (mol) for amount of substance, and the candela (cd) for luminous intensity.
Supplementary units:
Supplementary units are units used in the SI system to express derived physical quantities. The two supplementary units in the SI system are the radian (rad) for plane angle and the steradian (sr) for solid angle.
Derived physical quantities and derived units:
Derived physical quantities are physical quantities that can be expressed in terms of the seven fundamental physical quantities. Derived units are the units used to express these derived physical quantities. Examples of derived physical quantities include velocity, acceleration, force, pressure, energy, power, and electric charge. The units used to express these quantities are formed by combining the base units and supplementary units in various ways. For example, velocity is expressed in meters per second (m/s).
Physical quantities without units:
Some physical quantities do not have units, such as angles and ratios. These quantities are expressed as pure numbers and are dimensionless. For example, the coefficient of friction is a dimensionless quantity expressed as a ratio of two forces.
Multiples and submultiples of units:
In order to express physical quantities that are very large or very small, multiples and submultiples of units are used. These are formed by adding prefixes to the base units. For example, kilo (k) means 1000 times the base unit, while milli (m) means 1/1000 of the base unit. Some commonly used prefixes in the SI system include mega (M), giga (G), micro (μ), and nano (n).
Dimensions
Dimensions are an important aspect of physics that help us understand and analyze physical quantities. In this article, we will discuss the dimensions of basic physical quantities used in mechanics, dimensions of derived physical quantities, uses of dimensions, testing the correctness of a physical equation, finding the units of a given quantity, and deriving expressions.
Dimensions of basic physical quantities used in mechanics:
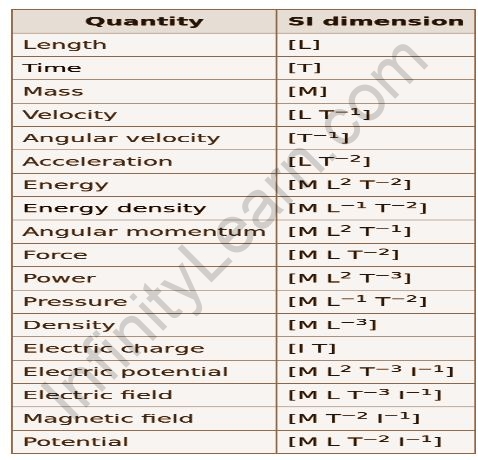
In mechanics, three fundamental physical quantities are used: mass, length, and time. These quantities have dimensions, which are represented by square brackets. The dimension of mass is denoted by [M], length by [L], and time by [T].
Mass:
The dimension of mass is [M]. This means that mass cannot be expressed in terms of length or time. The unit of mass in the SI system is the kilogram (kg).
Length:
The dimension of length is [L]. This means that length cannot be expressed in terms of mass or time. The unit of length in the SI system is the meter (m).
Time:
The dimension of time is [T]. This means that time cannot be expressed in terms of mass or length. The unit of time in the SI system is the second (s).
Dimensions of derived physical quantities:
Derived physical quantities are physical quantities that can be expressed in terms of the three fundamental physical quantities. The dimensions of derived physical quantities are obtained by combining the dimensions of the fundamental physical quantities in various ways. For example, the dimension of velocity is [L][T]^-1, which means that velocity can be expressed in terms of length and time.
Uses of dimensions:
Dimensions are useful for several purposes in physics. They can be used to test the correctness of a physical equation, find the units of a given quantity, and derive expressions.
Testing the correctness of a physical equation:
The principle of dimensional homogeneity states that the dimensions of each term in a physical equation must be the same. This means that the dimensions of the left-hand side of the equation must be equal to the dimensions of the right-hand side of the equation. This principle can be used to test the correctness of a physical equation. If the dimensions of each term are not the same, then the equation is not correct.
Finding the units of a given quantity:
Dimensions can also be used to find the units of a given physical quantity. For example, if the dimension of a physical quantity is [L][T]^-2, then the unit of the quantity can be expressed in terms of meters and seconds squared.
Deriving expressions:
Dimensions can also be used to derive expressions for physical quantities. For example, if the velocity of an object is given by v = at, where a is the acceleration and t is the time, then the dimensions of v are [L][T]^-1, the dimensions of a are [L][T]^-2, and the dimensions of t are [T]. By using dimensional analysis, we can derive an expression for the acceleration in terms of the velocity and time.
Measuring instrument
Measuring instruments are devices used to measure physical quantities accurately. In this article, we will discuss the principle, least count, and range of measuring instruments, errors of measurement, laboratory measuring instruments, and laboratory practicals using measuring instruments.
Principle, least count, and range:
The principle of a measuring instrument is the physical concept on which the instrument is based. For example, a vernier caliper works on the principle of the vernier scale, while a micrometer screw gauge works on the principle of the screw gauge.
The least count of a measuring instrument is the smallest value that can be measured by the instrument. It is determined by the precision of the instrument and the scale markings on the instrument. For example, the least count of a vernier caliper is 0.1 mm, while the least count of a micrometer screw gauge is 0.01 mm.
The range of a measuring instrument is the maximum value that can be measured by the instrument. For example, the range of a metre ruler is 1 meter, while the range of a vernier caliper is usually around 20 cm.
Errors of measurement:
Errors of measurement are deviations between the measured value and the true value of a physical quantity. There are two types of errors of measurement: systematic errors and random errors.
Systematic error:
Systematic errors are errors that occur due to the instrument's imperfections or the environment in which the measurement is taken. These errors are consistent and can be corrected by calibration of the instrument or by eliminating the source of the error.
Random error:
Random errors are errors that occur due to unpredictable and uncontrollable factors, such as natural fluctuations in the quantity being measured. These errors can be reduced by taking multiple measurements and calculating the average value.
Fractional error and percentage error:
Fractional error is the difference between the measured value and the true value, divided by the true value. Percentage error is the fractional error, expressed as a percentage. These measures are used to express the accuracy of a measurement.
Laboratory measuring instruments:
There are various laboratory measuring instruments, such as a metre ruler, vernier calipers, micrometer screw gauge, spherometer, travelling microscope, triple beam balance, digital multimeter, and stop clock/stopwatch.
Metre ruler:
A metre ruler is used to measure length up to 1 meter, with a least count of 1 mm.
Vernier calipers:
Vernier calipers are used to measure length up to 20 cm, with a least count of 0.1 mm. They have a main scale and a vernier scale, which allows for more precise measurements.
Micrometer screw gauge:
Micrometer screw gauges are used to measure length up to 25 mm, with a least count of 0.01 mm. They consist of a screw gauge and a thimble, which allows for very precise measurements.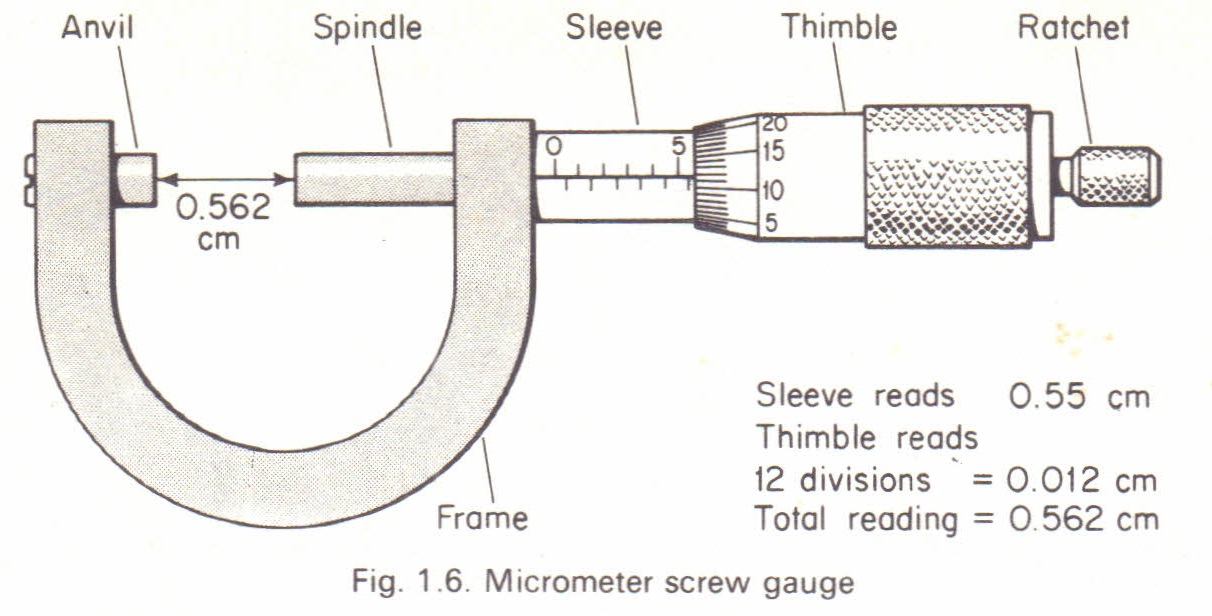
Spherometer:
A spherometer is used to measure the radius of curvature of a curved surface. It consists of a base with three legs and a central screw, which allows for very precise measurements.
Travelling microscope:
A travelling microscope is used to measure small lengths and small changes in length. It consists of a microscope and a moving stage, which allows for very precise measurements.
Triple beam balance/Four beam balance/Scientific electronic balance:
A triple beam balance, four beam balance, or scientific electronic balance is used to measure mass. These instruments have different least counts and ranges, and the electronic balance can measure very small masses with great precision.
Stop clock/stopwatch/Digital stopwatch:
A stop clock, stopwatch, or digital stopwatch is used to measure time. They have different least counts and ranges, and the digital stopwatch can measure very short time intervals with great precision.
Digital multimeter
A digital multimeter is an instrument used to measure various electrical quantities, such as voltage, current, and resistance. It has a digital display that provides a more accurate measurement than an analog multimeter.
Laboratory practicals using measuring instruments:
To perform laboratory practicals using measuring instruments, you must follow the correct procedures and use the appropriate instruments for the task.
Vernier calipers:
To use vernier calipers, you must ensure that the calipers are clean and the jaws are properly aligned. You must place the object to be measured between the jaws and read the measurement from the vernier scale and the main scale.
Micrometer screw gauge:
To use a micrometer screw gauge, you must ensure that the screw and thimble are clean and properly aligned. You must place the object to be measured between the anvil and spindle and turn the thimble until the object is firmly gripped. You must read the measurement from the main scale and the thimble scale.
Spherometer:
To use a spherometer, you must ensure that the legs are clean and properly aligned. You must place the spherometer on the curved surface and turn the central screw until the legs just touch the surface. You must read the measurement from the central screw and the leg screws.
Travelling microscope:
To use a travelling microscope, you must ensure that the microscope is clean and properly aligned. You must place the object to be measured on the stage and adjust the focus until the image is clear. You must then move the stage until the object is at the desired position and read the measurement from the microscope scale.
Scalers and Vectors
Scalars and vectors are two important concepts in physics that are used to represent physical quantities. Scalar quantities are those that are completely described by their magnitude, while vector quantities have both magnitude and direction.
Scalar quantities:
Examples of scalar quantities include time, mass, temperature, distance, and speed. Scalar quantities can be added, subtracted, multiplied, and divided just like regular numbers.
Vector quantities:
Examples of vector quantities include displacement, velocity, acceleration, force, and momentum. Vector quantities can be represented graphically by arrows, where the length of the arrow represents the magnitude of the vector and the direction of the arrow represents the direction of the vector.
Geometrical representation of a vector quantity:
Vectors can be represented geometrically by drawing an arrow to represent the vector. The length of the arrow represents the magnitude of the vector, and the direction of the arrow represents the direction of the vector.
Resultant vector of two vectors in the same line and parallel lines:
When two vectors are in the same line and pointing in the same direction, the resultant vector is the sum of the magnitudes of the two vectors. When two vectors are parallel but pointing in opposite directions, the resultant vector is the difference between the magnitudes of the two vectors.
Two inclined vectors:
When two vectors are inclined at an angle to each other, the resultant vector can be found using the parallelogram law or the triangle method.
Parallelogram law:
The parallelogram law states that the resultant vector of two vectors can be found by drawing a parallelogram using the two vectors as adjacent sides. The diagonal of the parallelogram is the resultant vector.
Triangle method:
The triangle method is similar to the parallelogram law, but instead of drawing a parallelogram, a triangle is drawn using the two vectors as two sides. The third side of the triangle is the resultant vector.
System of vectors:
A system of vectors is a collection of vectors that are acting on an object at the same time. The resultant vector of a system of vectors is the vector that represents the net effect of all the individual vectors.
Polygon method:
The polygon method is used to find the resultant vector of a system of vectors. The individual vectors are drawn as sides of a polygon, and the closing side of the polygon is the resultant vector.
Resolution of vectors:
Resolution of vectors is the process of breaking down a vector into its component parts along two or more mutually perpendicular axes. The component parts are scalar quantities and can be added, subtracted, multiplied, and divided just like regular numbers.
Studying the above article on units and measurements, dimensions,
measuring instruments, and scalars and vectors in physics can provide
several benefits to the readers. Understanding the physical quantities
and units, fundamental physical quantities, SI units, and derived
physical quantities and units can help students in comprehending various
physical concepts and performing accurate measurements in different
fields of physics. Knowing about the dimensions of basic and derived
physical quantities can enable learners to evaluate physical equations
and develop expressions. Familiarity with different measuring
instruments, their principles, least count, range, and errors can enable
students to perform precise measurements in laboratory experiments.
Understanding the distinction between scalar and vector quantities and
the methods to calculate the resultant vector can be useful in solving
problems related to forces, motion, and other vector quantities.
Overall, the knowledge gained from this article can help students in
enhancing their understanding of physics, making accurate measurements,
and solving problems related to physical quantities and vectors.
Download our latest updated app "Advanced level physics" for physics lesson revisions
Physics revision notes for JEE, NEET, Advanced level Sri Lanka.
Advanced
level physics app provides an interactive learning environment to
revise physics theory. This will be a perfect guide to prepare for
Advanced level examination in Sri Lanka.
Below lessons are summarized within the app to guide you through physics problems.
Solving problems while referring the app, helps understanding principle.
Works offline.
1.Units and dimensions
2.Mechanics
3.Oscillations and waves
4.Thermal statics
5.Thermal dynamics

